In September, I wrote about the fundamental group of a topos, but I didn’t yet give an example of how to compute this fundamental group for toposes of the form \(\mathbf{Sh}(X)\) for \(X\) a topological space. If \(X\) is a CW-complex, then the fundamental group of \(\mathbf{Sh}(X)\) agrees with the (discrete) group \(\pi_1(X)\). On the other hand, if \(X\) is the shrinking wedge of circles, then the fundamental group of \(\mathbf{Sh}(X)\) is not discrete, so this is an interesting example to look at.
Note: I have changed the terminology in this blogpost from “Hawaiian earring” to “shrinking wedge of circles”, following Hawaiian mathematicians and others who spoke out against the harmful terminology.
Before starting the computation…
Can the fundamental group of \(\mathbf{Sh}(X)\) be \(\mathrm{Gal}(\bar{\mathbb{Q}}/\mathbb{Q})\)?
I now (almost) know the solution to one of the questions that I had earlier. The question was: given a profinite group \(G\), can we find a connected, locally connected topological space \(X\) such that \(G\) is the fundamental group of \(\mathbf{Sh}(X)\)? Here \(X\) cannot be a “nice” space like a CW-complex, otherwise the fundamental group of \(\mathbf{Sh}(X)\) is the discrete group \(\pi_1(X)\).
A solution is given by Brazas in “The fundamental group as a topological group”, Theorem 4.10. There it is shown that any topological group arises as \(\pi_1^\tau(X)\) of some topological space \(X\), where \(\pi_1^\tau(X)\) is \(\pi_1(X)\) equipped with a natural topology related to the compact-open topology on the space of loops.
If \(X\) is connected, locally connected, we can recover the fundamental group of \(\mathbf{Sh}(X)\) from \(\pi_1^\tau(X)\). The underlying group is \(\pi_1(X)\), and the basic open subsets are cosets of open normal subgroups in \(\pi_1^\tau(X)\). The fundamental group of a topos is only determined up to Morita equivalence though, so there can be non-isomorphic topological groups that both qualify as fundamental group for \(\mathbf{Sh}(X)\).
Back to the question… Suppose that \(G\) is a profinite group. Take a space \(X\) such that \(\pi_1^\tau(X) = G\). Because \(G\) is profinite, the open sets are already unions of cosets of open normal subgroups. So \(G\) is the fundamental group of \(\mathbf{Sh}(X)\).
There’s a small caveat here. For topos-theoretic purposes, the space \(X\) should be locally connected, which is not necessarily the case if applying Theorem 4.10 of “The fundamental group as a topological group”. But probably the argument can be modified to make sure that \(X\) is locally connected. Another way around this is to define fundamental groups for toposes that are not necessarily locally connected, but I don’t know yet if/why that makes sense.
I am thankful to Jeremy Brazas (@jtbrazas) for helping me understand his paper. If you want to know more about this, I can also recommend his paper “Semicoverings: a generalization of covering space theory” and his blog Wild Topology.
Covering spaces of the shrinking wedge of circles
Now, let’s have a look at how to compute the fundamental group of \(\mathbf{Sh}(X)\), for \(X\) the shrinking wedge of circles. We will do this by explicitly classifying the covering spaces of \(X\). Then we will construct a topological group \(G\) such that the connected covering spaces of \(X\) correspond to the transitive group actions of \(G\). It follows that \(G\) is the fundamental group of \(\mathbf{Sh}(X)\).
The fundamental group of \(\mathbf{Sh}(X)\) is not determined up to isomorphism, but only up to Morita equivalence. As described above, you could equivalently find a fundamental group of \(\mathbf{Sh}(X)\) by equipping \(\pi_1(X)\) with a suitable topology. But if \(X\) is the shrinking wedge of circles, then \(\pi_1(X)\) is uncountable. On the other hand, the fundamental group of \(\mathbf{Sh}(X)\) that we will construct below is countable. Conclusion: if two topological groups are Morita equivalent, this doesn’t mean that they have the same cardinality.
Here is the shrinking wedge of circles:
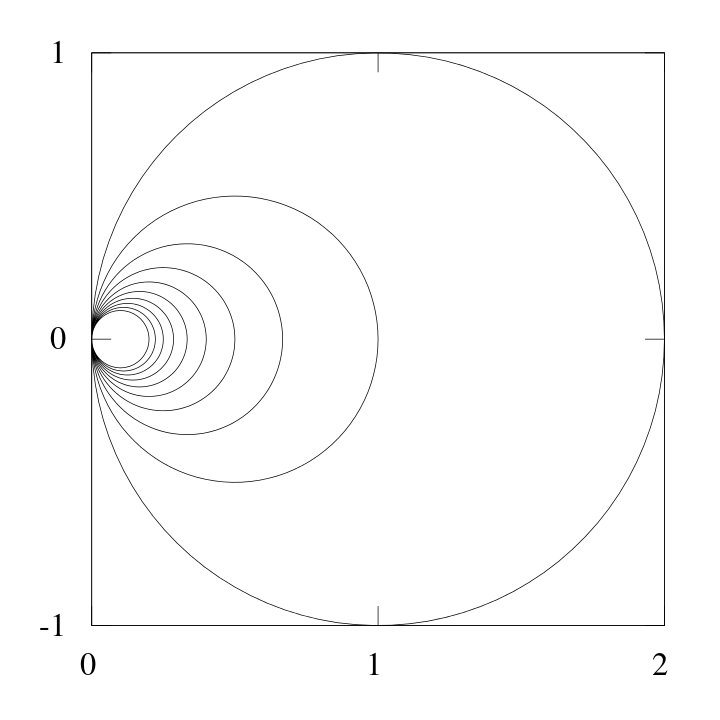
It is the union of infinitely many circles: for each nonzero natural number \(n\), it contains a circle of radius \(\tfrac{1}{n}\) that goes through the origin. The topology is the subspace topology from \(\mathbb{R}^2\).
Suppose that \(\pi : Y \to X\) is a covering space, with \(X\) the shrinking wedge of circles. Then there is some open covering \(\{U_i\}_{i \in I}\) of \(X\), such that for each \(i \in I\) the map \(\pi^{-1}(U_i) \to U_i\) is a trivial covering space. Here “trivial covering space” means that \(\pi^{-1}(U_i) = \bigsqcup_{j \in S} U_i\) for some index set \(S\), and that the projection \(\pi^{-1}(U_i)\) is the identity on each component.

One of these open sets \(U_i\) above must contain the origin. But then it contains everyting within some distance \(\varepsilon\) from the origin, so it contains all circles of the shrinking wedge of circles, except maybe finitely many of them.
This part \(U_i\) of the shrinking wedge of circles, close to the origin and containing almost all circles, is the most difficult part… and we now know that nothing interesting happens with this part, in the sense that \(\pi^{-1}(U_i) \to U_i\) is a trivial covering space. So we can ignore this part, and pretend that the shrinking wedge of circles is just a union of finitely many circles.
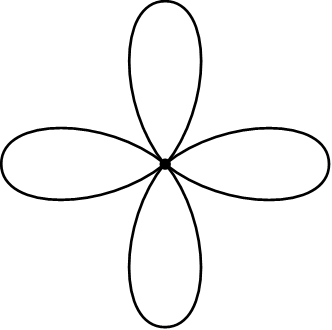
This subspace consisting of finitely many circles is called a rose, and each circle is called a petal (so the image above is the rose with four petals). Because a rose is a semilocally simply connected space, we know that the covering spaces correspond to sets with an action of the fundamental group. This means that if \(R\) is the rose with \(n\) petals, then to reconstruct a covering map \(\pi : Q \to R\) we only need to remember the fiber \(F= \pi^{-1}(x_0)\), where \(x_0\) is the center of the rose, and the action of \(\pi_1(R)\) on \(F\).

In our case, \(\pi_1(R)\) is the free group on \(n\) variables. So a covering space is equivalently a set \(F\), together with for each \(i \in \{1,\dots,n\}\) an automorphism \(\alpha_i : F \to F\). Each \(\alpha_i\) corresponds to a loop \(\gamma_i\) that goes around exactly one petal.
If one of the automorphisms \(\alpha_i\) is the identity, then this means that nothing happens with the corresponding loop \(\gamma_i\). In other words, the restriction to \(\gamma_i\) of the covering map \(\pi : Q \to R\), given by \(\pi^{-1}(\gamma_i) \to \gamma_i\), is a trivial covering map.
If this is the case, then we can ignore \(\gamma_i\), just like how we ignored most petals/circles for the shrinking wedge of circles.
We can go in the other direction as well. Each covering space for the rose with \(n\) petals gives a covering space for the rose with \(n+1\) petals. It’s just that nothing happens with the \((n+1)\)-th petal. In terms of the set \(F\) with action of the fundamental group, we have that the permutation \(\alpha_{n+1} : F \to F\) is trivial.
Going back to the shrinking wedge of circles \(X\), this means that a covering space \(\pi : Y \to X\) is given by a set \(F\) together with infinitely many automorphisms/permutations \(\alpha_1, \alpha_2, \alpha_3, \dots\) of \(F\), one for each circle, with the special property that only finitely many of these automorphisms are nontrivial.
Topos fundamental group of the shrinking wedge of circles
We now know that a covering space of the shrinking wedge of circles corresponds to a set \(F\) with infinitely permutations \(\alpha_1,\alpha_2,\alpha_3,\dots\) such that only finitely many of them are nontrivial.
The fundamental group \(G\) of the associated topos will have as underlying group the free group on infinitely many generators \(\gamma_1, \gamma_2, \gamma_3, \dots\) Further, we need to equip \(G\) with a topology with the special property that a transitive action of \(G\) on a set \(F\) is continuous if and only if only finitely many \(\gamma_i\)’s act nontrivially.
Let’s try to construct such a topology. We define a subset \(U \subseteq G\) to be open if and only if it has the following property: for all \(h \in U\), there is some natural number \(N\) such that \(h\gamma_n \in U\) and \(h\gamma_n^{-1}\in U\) for all \(n \geq N.\) It is not so difficult to check that this satisfies the axioms for a topology. With some more work, you can check that the topology is compatible with the group structure.
With this topology, a subgroup is open if and only if it contains all elements \(\gamma_n\), except maybe finitely many of them. So the transitive group actions are precisely the ones such that almost all elements \(\gamma_n\) act trivially.
So the topological group \(G\) that we constructed is the fundamental group of \(\mathbf{Sh}(X)\) , the topos of sheaves on the shrinking wedge of circles. In particular, there is a (connected) geometric morphism \(\mathbf{Sh}(X) \longrightarrow \mathbf{Cont}(G)\) to the topos of continuous \(G\)-sets. The inverse image functor sends a set with transitive, continuous \(G\)-action to its corresponding covering space of the shrinking wedge of circles.
