Patterns made by the reducible quadratic polynomials modulo n

by Jens Hemelaer

3 min read October 4, 2019

Take a natural number \(n \geq 2\). Then we can create an interesting pattern as follows: we draw a dot with coordinates \((b,c)\) if the polynomial \(x^2+bx+c\) is reducible modulo \(n\). In other words, we draw a dot on \((b,c)\) if we can find natural numbers \(x_1\) and \(x_2\) such that \(b-x_1-x_2\) and \(c-x_1 x_2\) are both divisible by \(n\). This pattern repeats itself vertically and horizontally.

This is the result for \(n=5\):

And for \(n=7\) we get:

In both cases, the pattern is repeated 25 times, and Python automatically draws each block in a different color (for the code, scroll down to the end of the post).

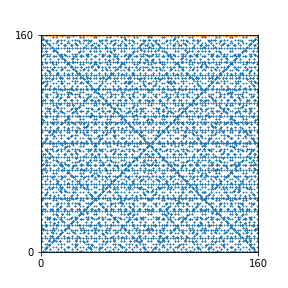
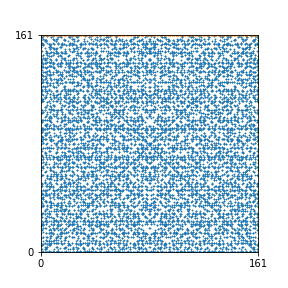
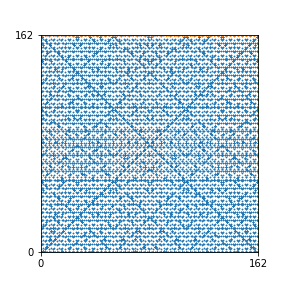
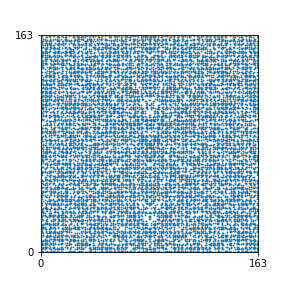
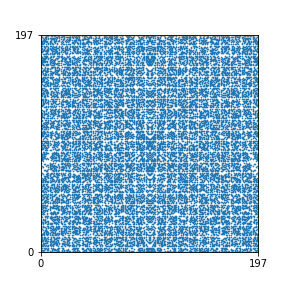
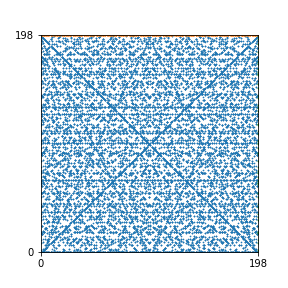
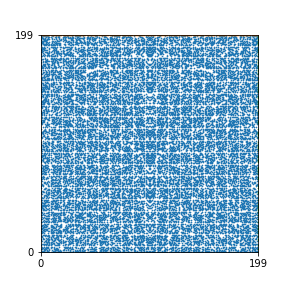
Here are the patterns for all numbers \(n\) starting at \(n=2\) and ending with \(n=199\) (with one “block” per pattern). It seems that the prime numbers have the most chaotic patterns…

$$n=2$$

$$n=3$$

$$n=4$$

$$n=5$$

$$n=6$$

$$n=7$$

$$n=8$$

$$n=9$$

$$n=10$$

$$n=11$$

$$n=12$$

$$n=13$$

$$n=14$$

$$n=15$$

$$n=16$$

$$n=17$$

$$n=18$$

$$n=19$$

$$n=20$$

$$n=21$$

$$n=22$$

$$n=23$$

$$n=24$$

$$n=25$$

$$n=26$$

$$n=27$$

$$n=28$$

$$n=29$$

$$n=30$$

$$n=31$$

$$n=32$$

$$n=33$$

$$n=34$$

$$n=35$$

$$n=36$$

$$n=37$$

$$n=38$$

$$n=39$$

$$n=40$$

$$n=41$$

$$n=42$$

$$n=43$$

$$n=44$$

$$n=45$$

$$n=46$$

$$n=47$$

$$n=48$$

$$n=49$$

$$n=50$$

$$n=51$$

$$n=52$$

$$n=53$$

$$n=54$$

$$n=55$$

$$n=56$$

$$n=57$$

$$n=58$$

$$n=59$$

$$n=60$$

$$n=61$$

$$n=62$$

$$n=63$$

$$n=64$$

$$n=65$$

$$n=66$$

$$n=67$$

$$n=68$$

$$n=69$$

$$n=70$$

$$n=71$$

$$n=72$$

$$n=73$$

$$n=74$$

$$n=75$$

$$n=76$$

$$n=77$$

$$n=78$$

$$n=79$$

$$n=80$$

$$n=81$$

$$n=82$$

$$n=83$$

$$n=84$$

$$n=85$$

$$n=86$$

$$n=87$$

$$n=88$$

$$n=89$$

$$n=90$$

$$n=91$$

$$n=92$$

$$n=93$$

$$n=94$$

$$n=95$$

$$n=96$$

$$n=97$$

$$n=98$$

$$n=99$$

$$n=100$$

$$n=101$$

$$n=102$$

$$n=103$$

$$n=104$$

$$n=105$$

$$n=106$$

$$n=107$$

$$n=108$$

$$n=109$$

$$n=110$$

$$n=111$$

$$n=112$$

$$n=113$$

$$n=114$$

$$n=115$$

$$n=116$$

$$n=117$$

$$n=118$$

$$n=119$$

$$n=120$$

$$n=121$$

$$n=122$$

$$n=123$$

$$n=124$$

$$n=125$$

$$n=126$$

$$n=127$$

$$n=128$$

$$n=129$$

$$n=130$$

$$n=131$$

$$n=132$$

$$n=133$$

$$n=134$$

$$n=135$$

$$n=136$$

$$n=137$$

$$n=138$$

$$n=139$$

$$n=140$$

$$n=141$$

$$n=142$$

$$n=143$$

$$n=144$$

$$n=145$$

$$n=146$$

$$n=147$$

$$n=148$$

$$n=149$$

$$n=150$$

$$n=151$$

$$n=152$$

$$n=153$$

$$n=154$$

$$n=155$$

$$n=156$$

$$n=157$$

$$n=158$$

$$n=159$$

$$n=160$$

$$n=161$$

$$n=162$$

$$n=163$$

$$n=164$$

$$n=165$$

$$n=166$$

$$n=167$$

$$n=168$$

$$n=169$$

$$n=170$$

$$n=171$$

$$n=172$$

$$n=173$$

$$n=174$$

$$n=175$$

$$n=176$$

$$n=177$$

$$n=178$$

$$n=179$$

$$n=180$$

$$n=181$$

$$n=182$$

$$n=183$$

$$n=184$$

$$n=185$$

$$n=186$$

$$n=187$$

$$n=188$$

$$n=189$$

$$n=190$$

$$n=191$$

$$n=192$$

$$n=193$$

$$n=194$$

$$n=195$$

$$n=196$$

$$n=197$$

$$n=198$$

$$n=199$$

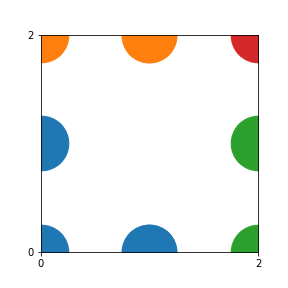
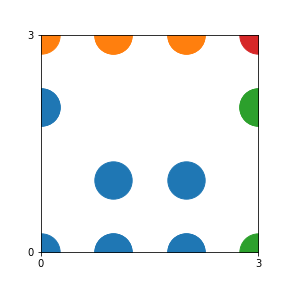
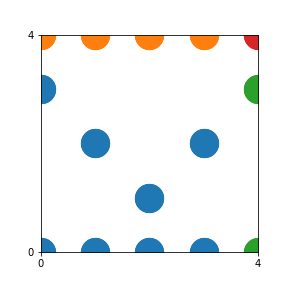
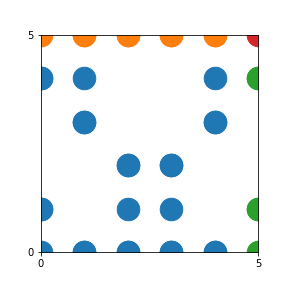
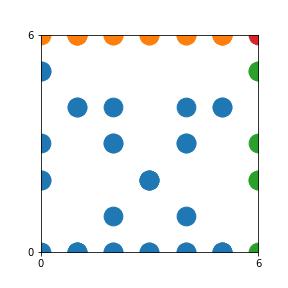
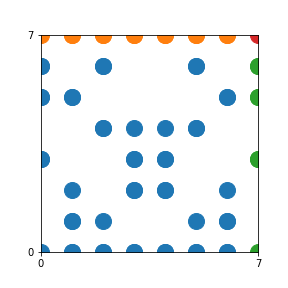
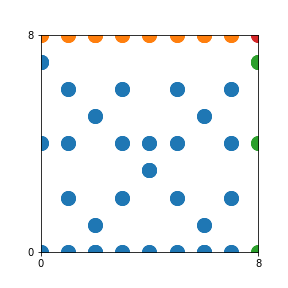
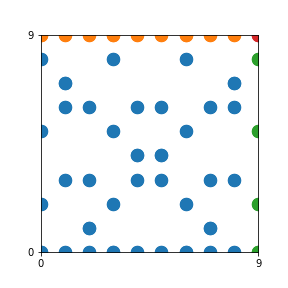
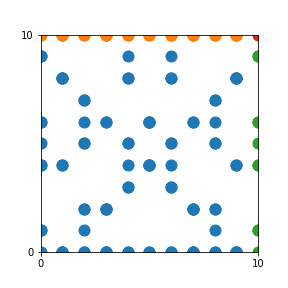
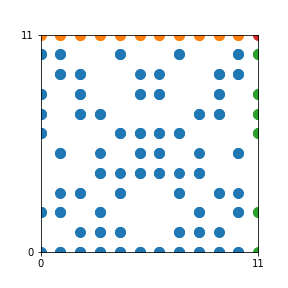
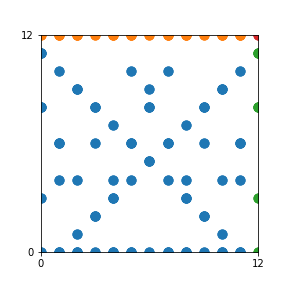
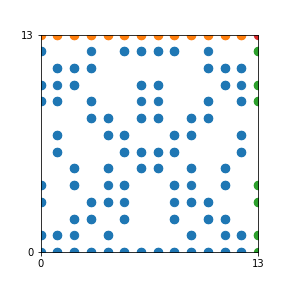
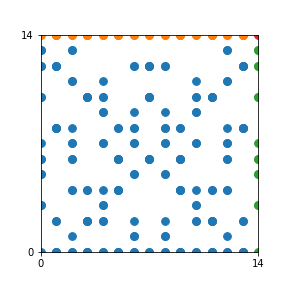
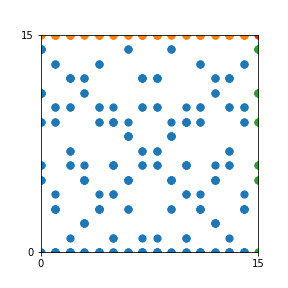
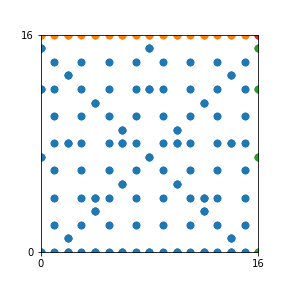
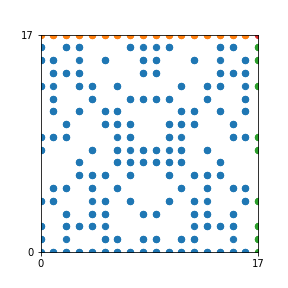
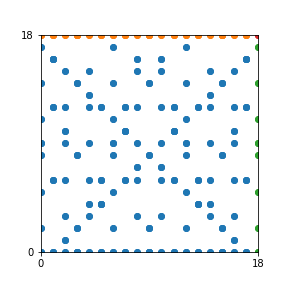
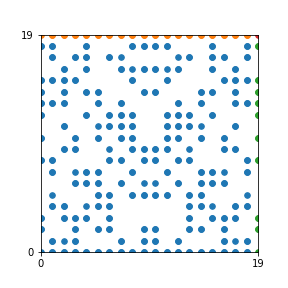
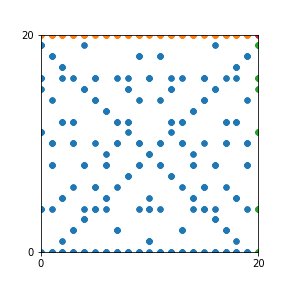
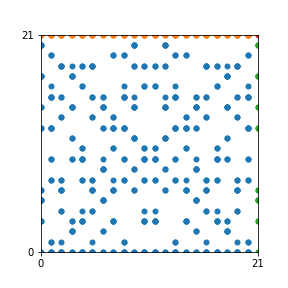
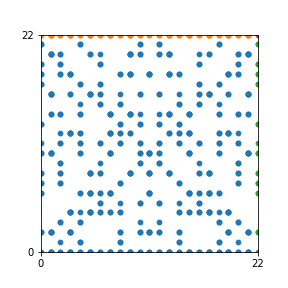
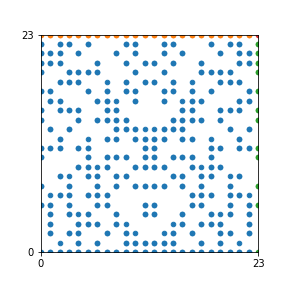
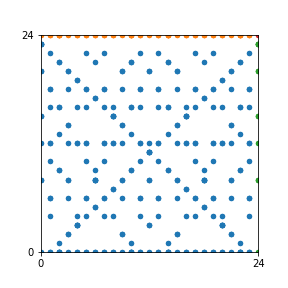
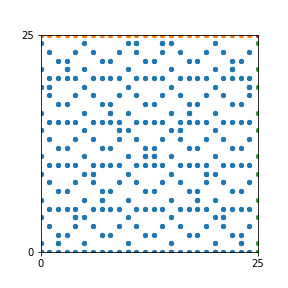
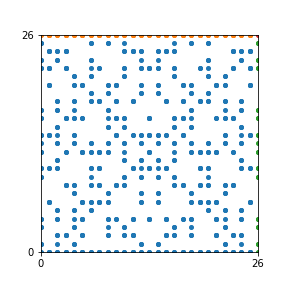
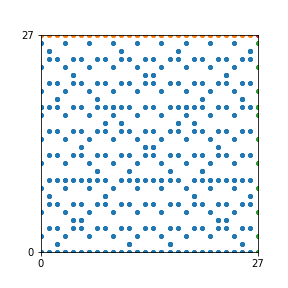
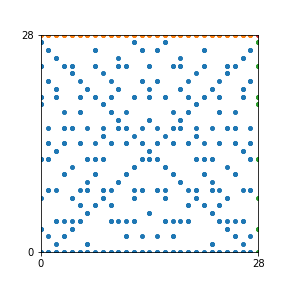
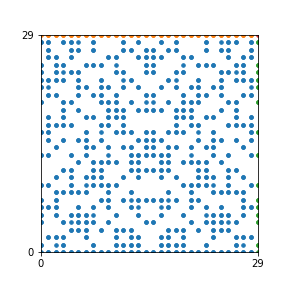
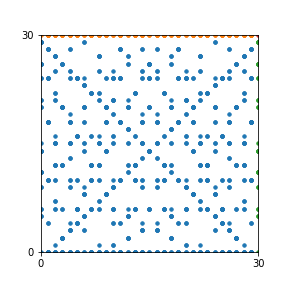
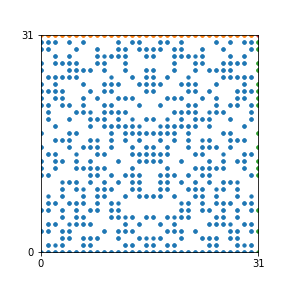
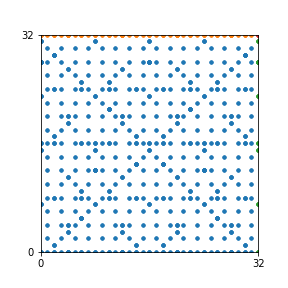
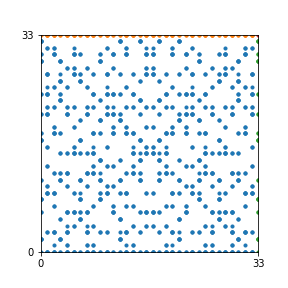
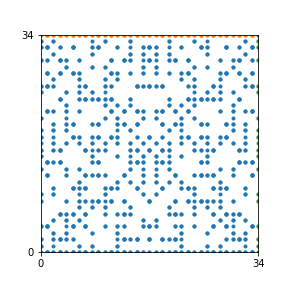
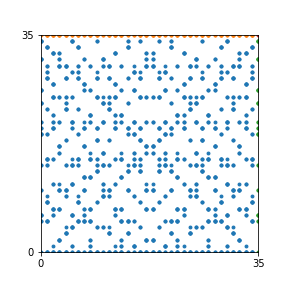
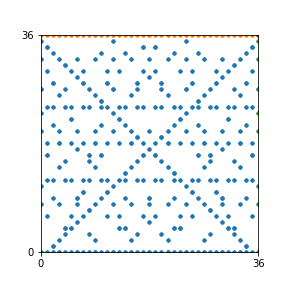
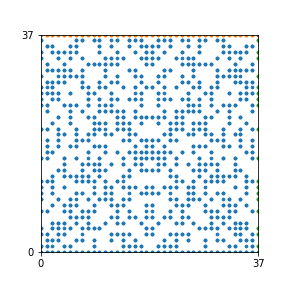
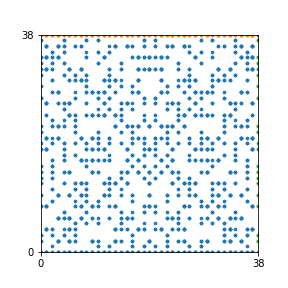
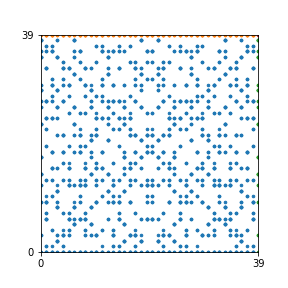
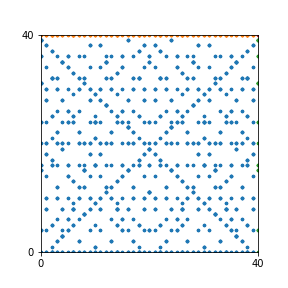
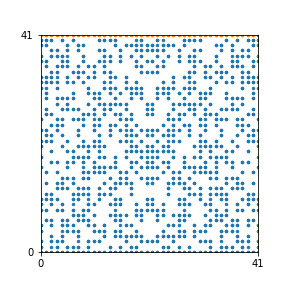
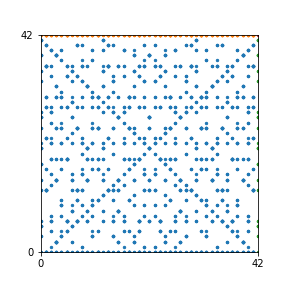
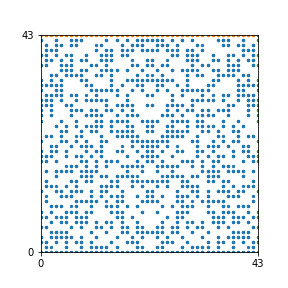
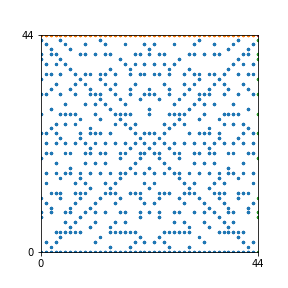
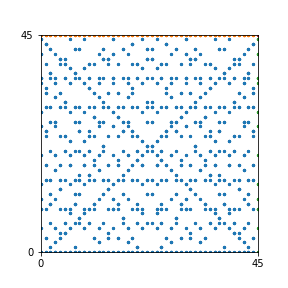
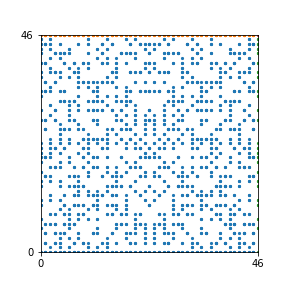
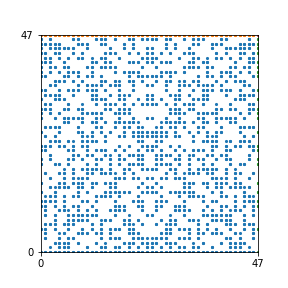
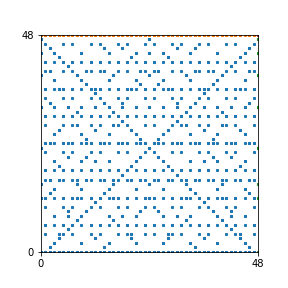
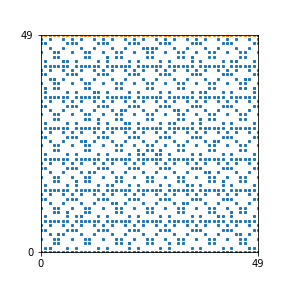
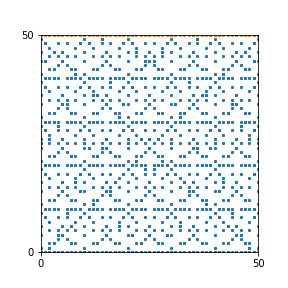
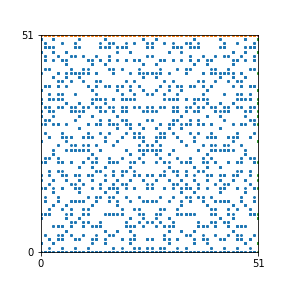
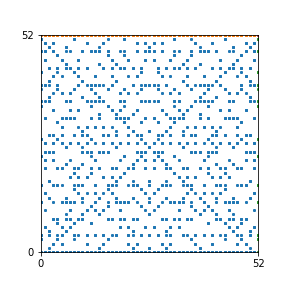
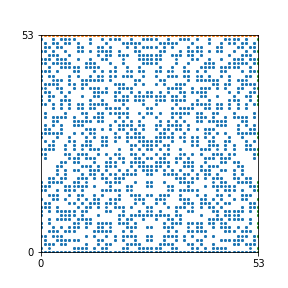
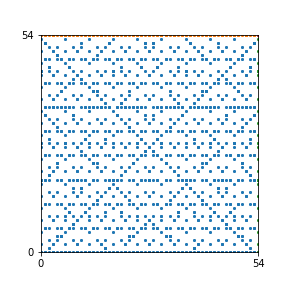
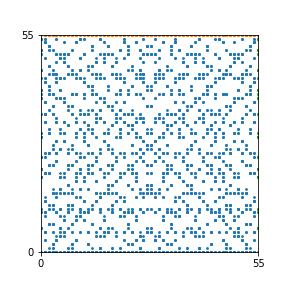
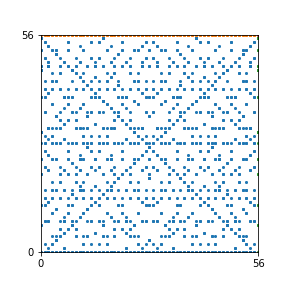
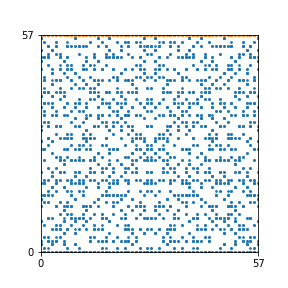
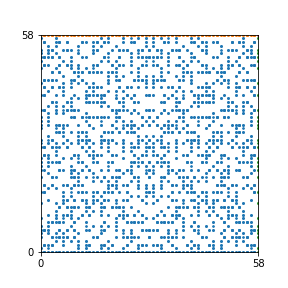
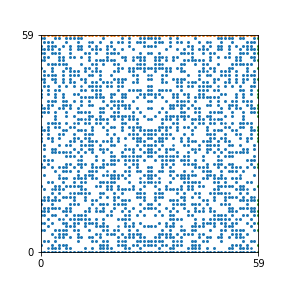
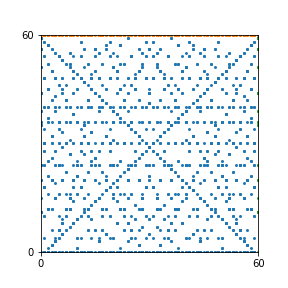
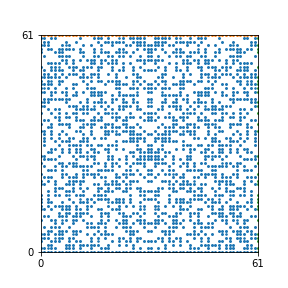
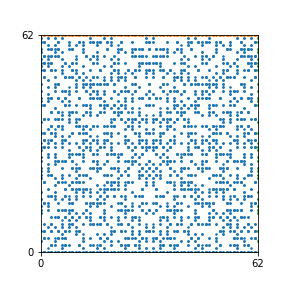
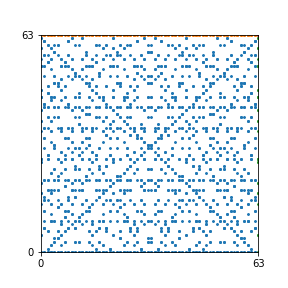
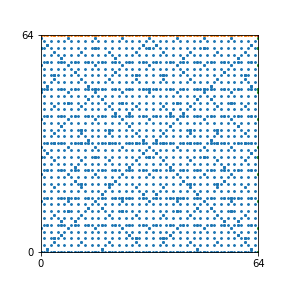
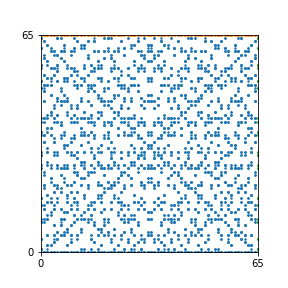
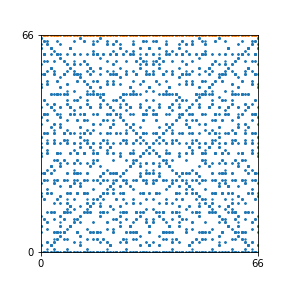
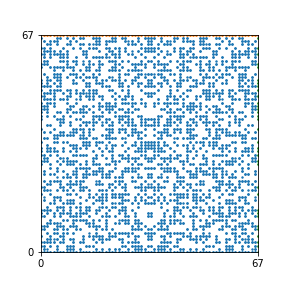
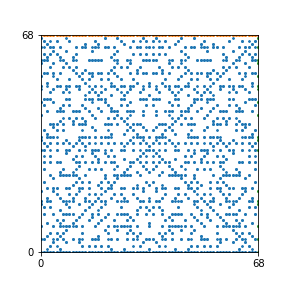
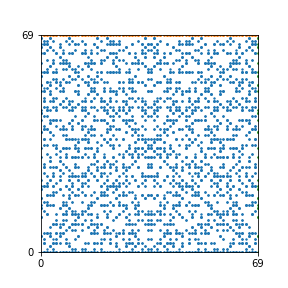
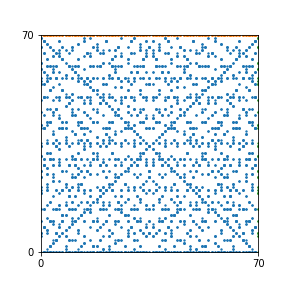
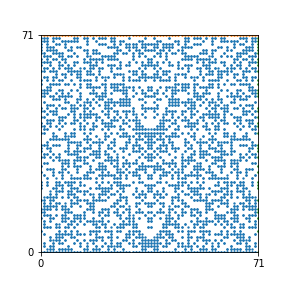
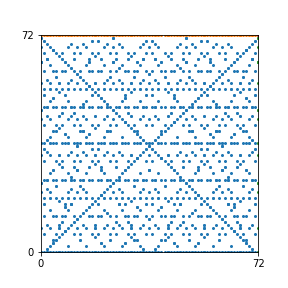
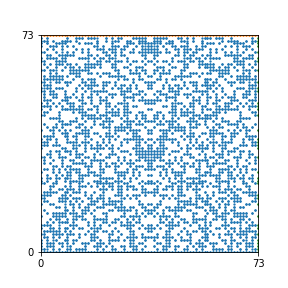
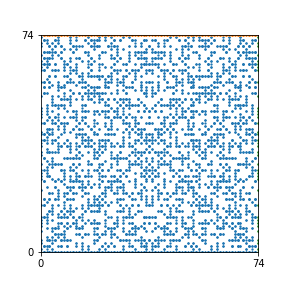
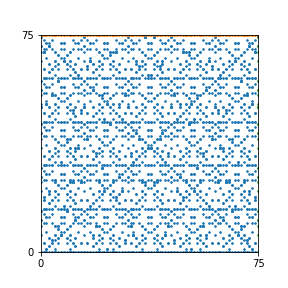
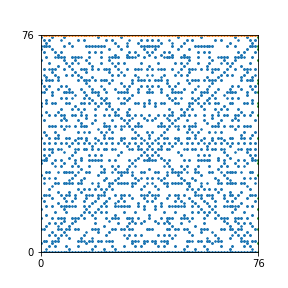
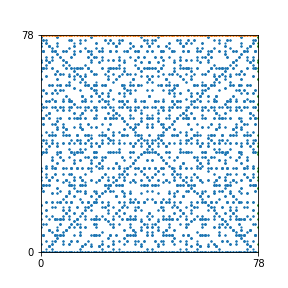
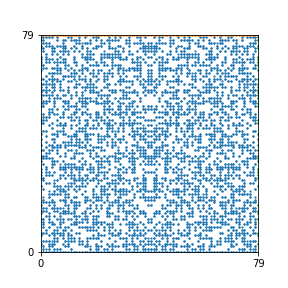
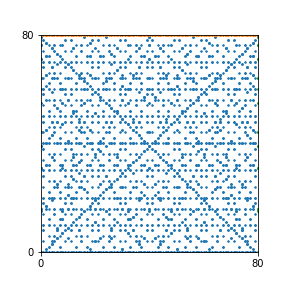
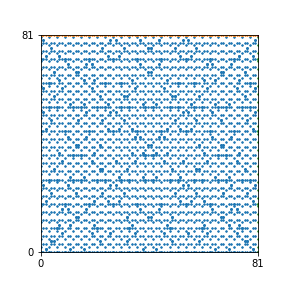
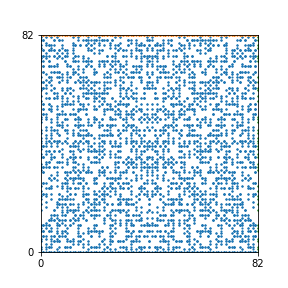
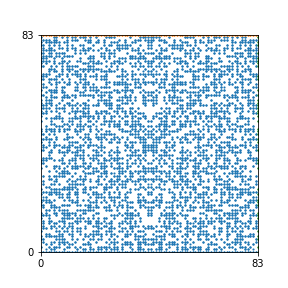
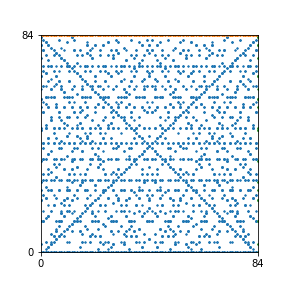
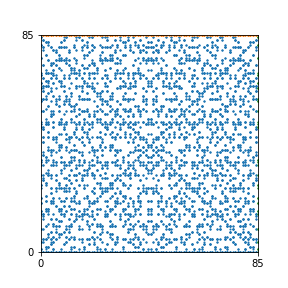
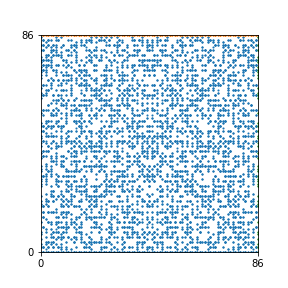
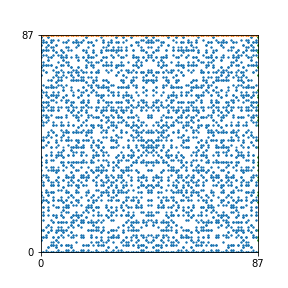
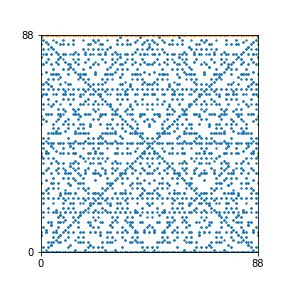
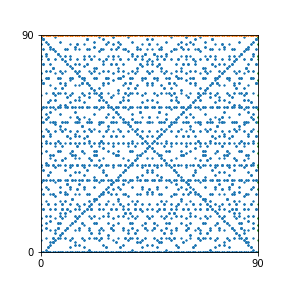
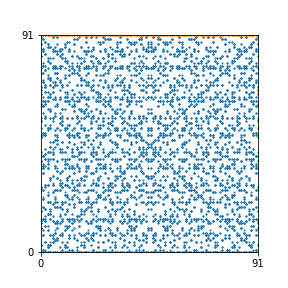
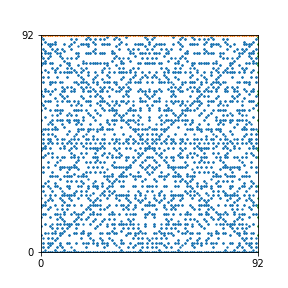
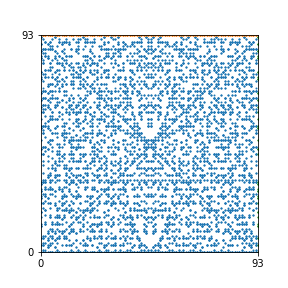
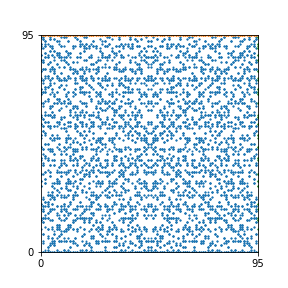
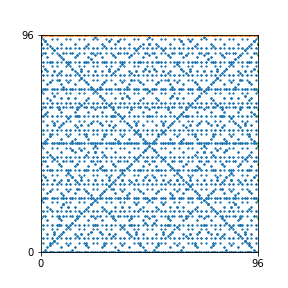
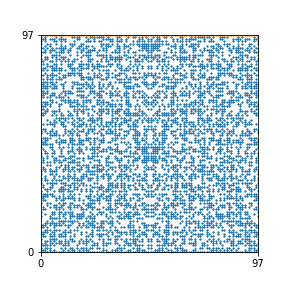
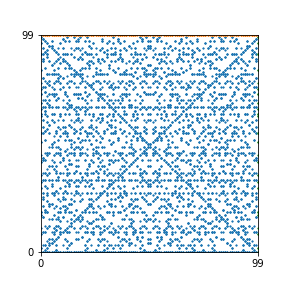
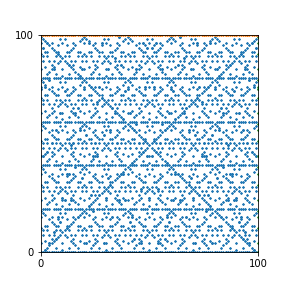
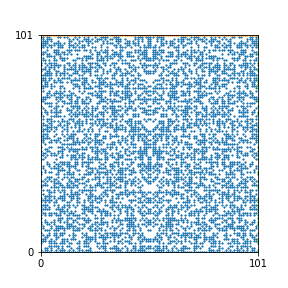
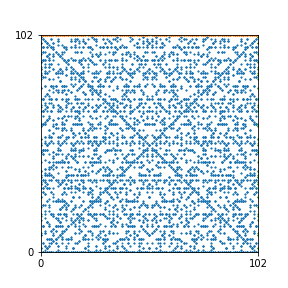
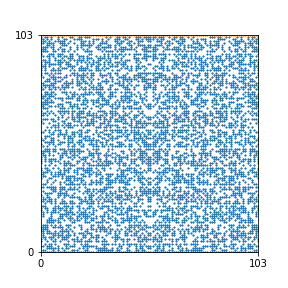
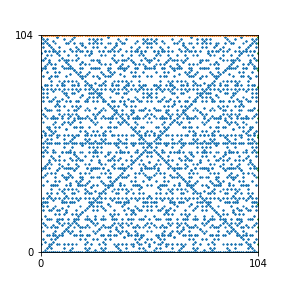
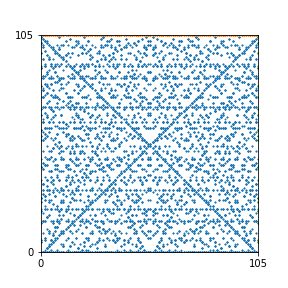
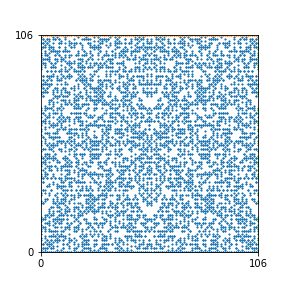
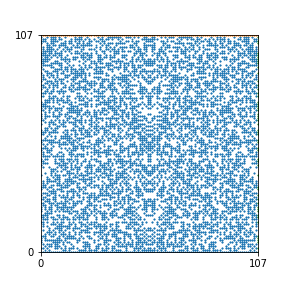
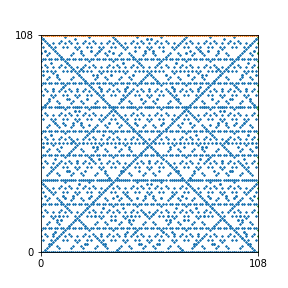
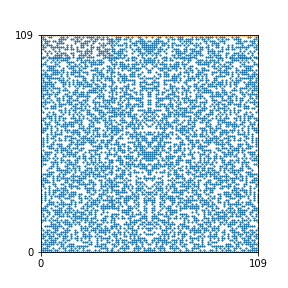
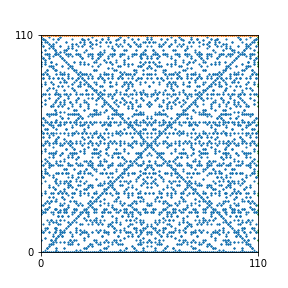
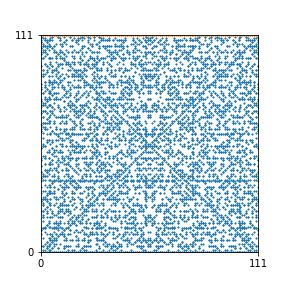
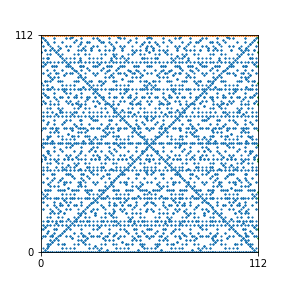
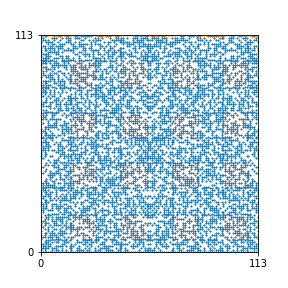
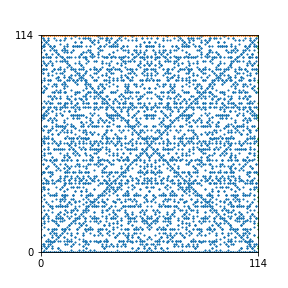
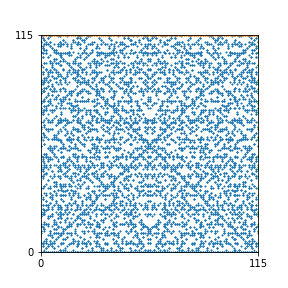
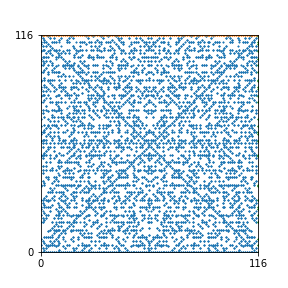
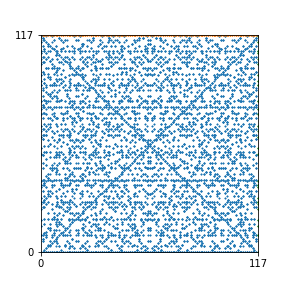
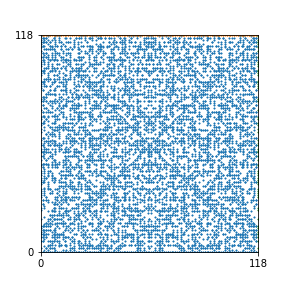
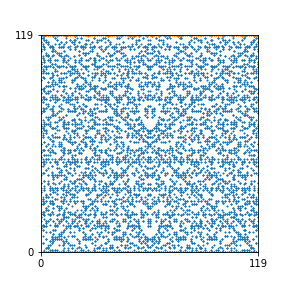
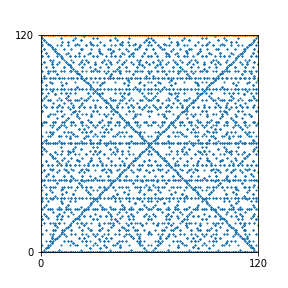
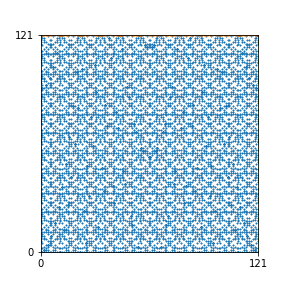
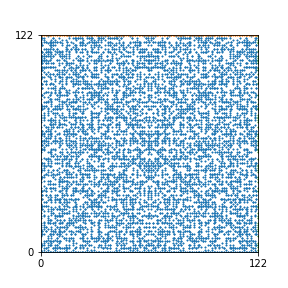
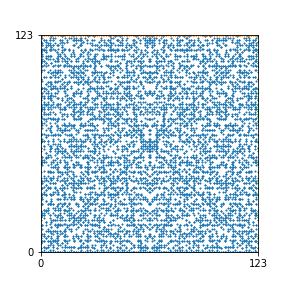
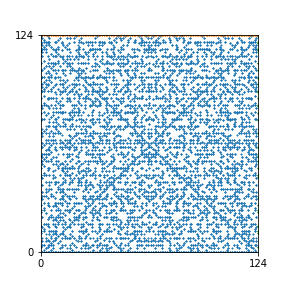
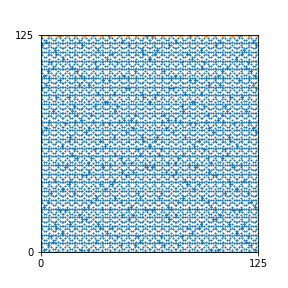
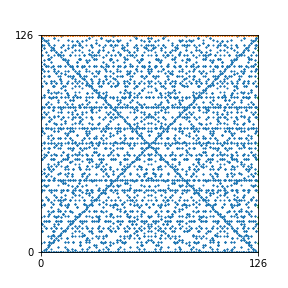
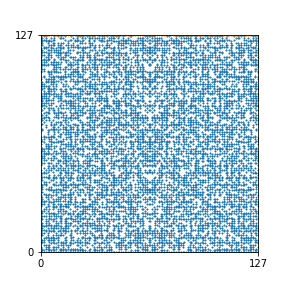
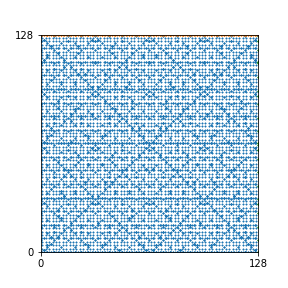
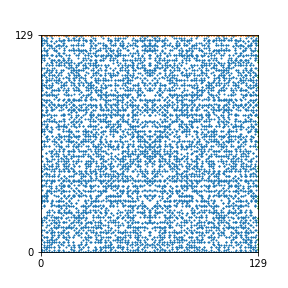
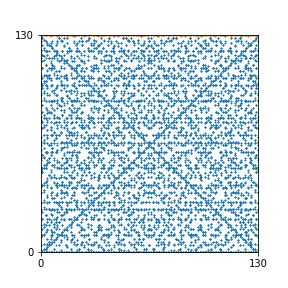
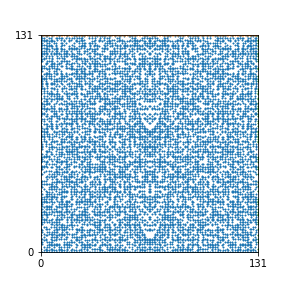
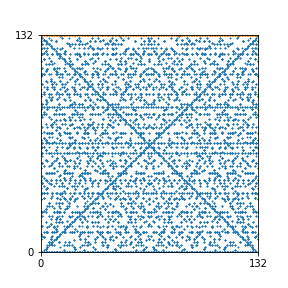
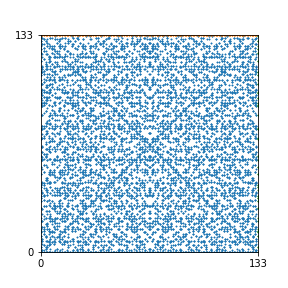
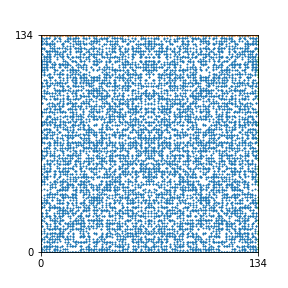
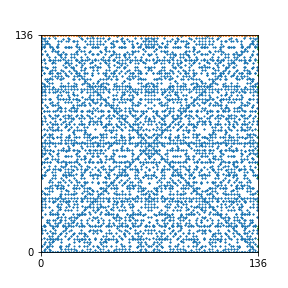
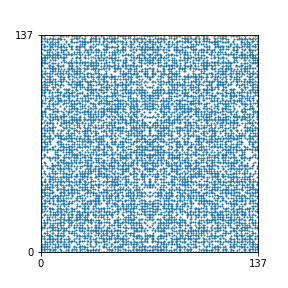
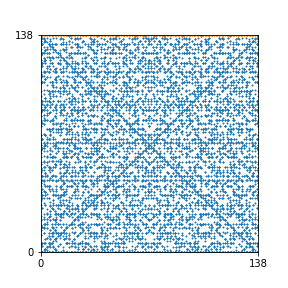
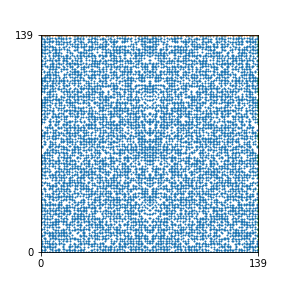
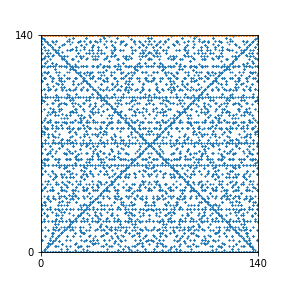
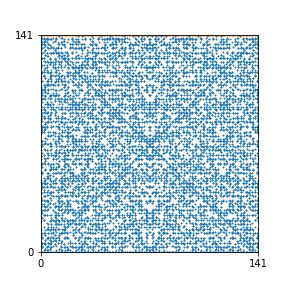
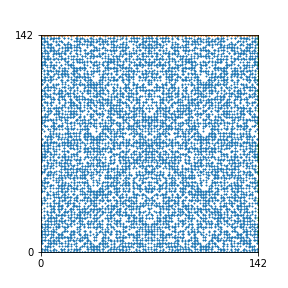
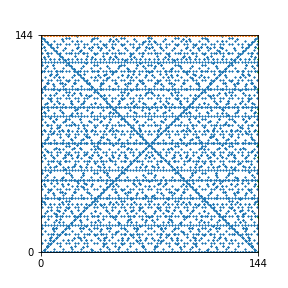
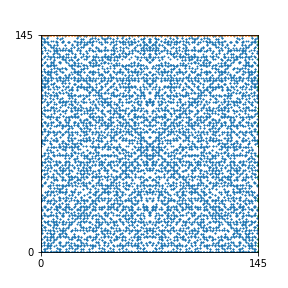
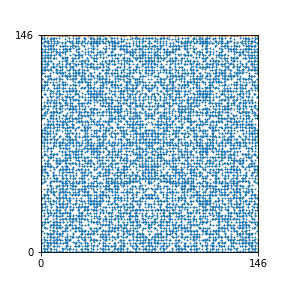
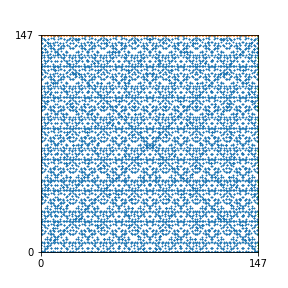
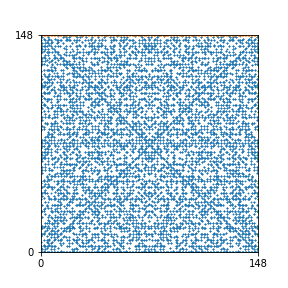
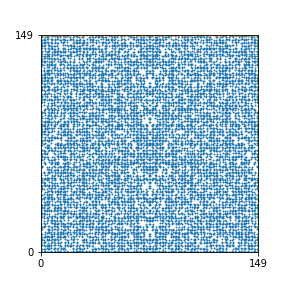
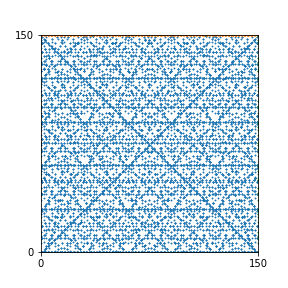
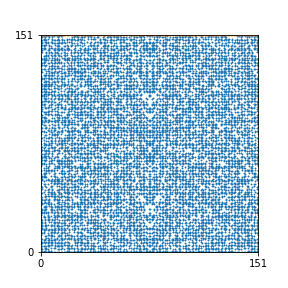
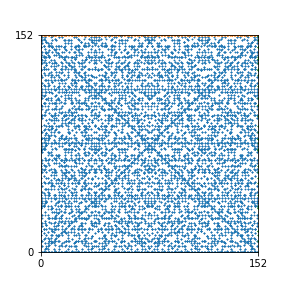
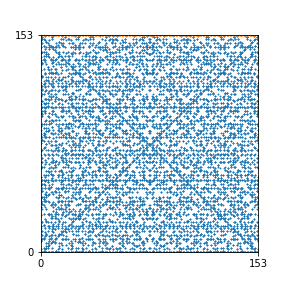
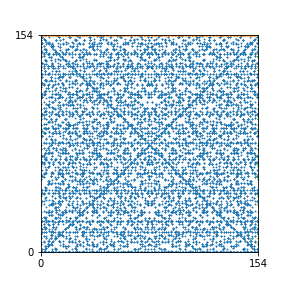
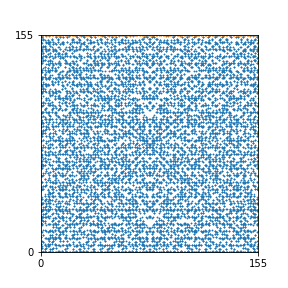
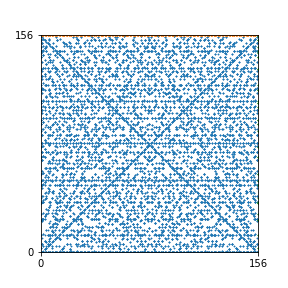
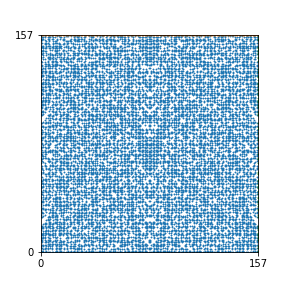
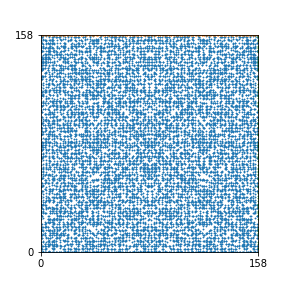
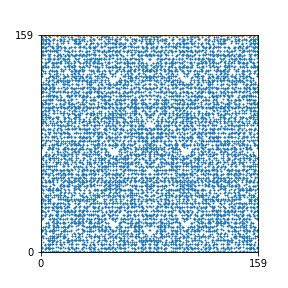
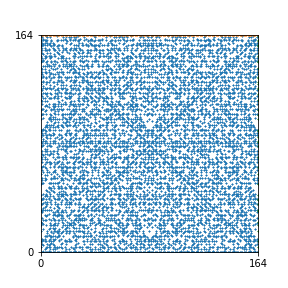
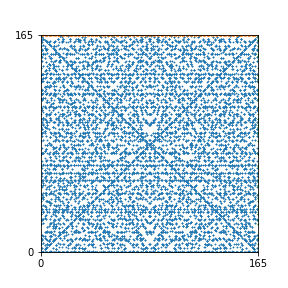
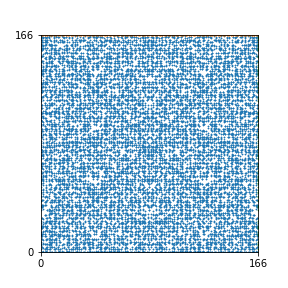
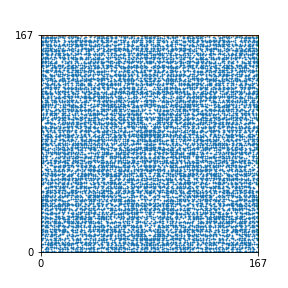
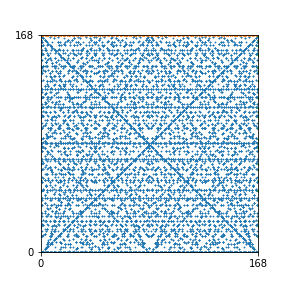
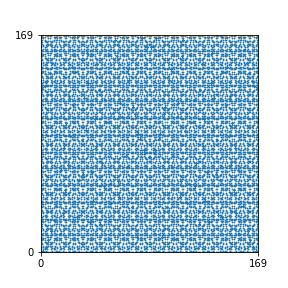
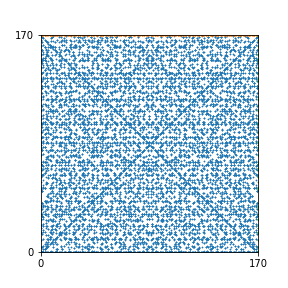
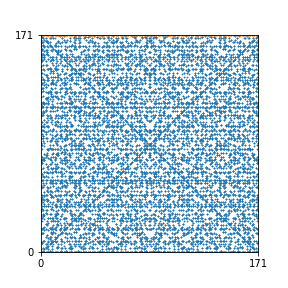
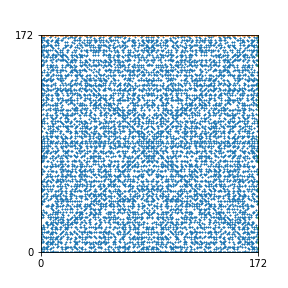
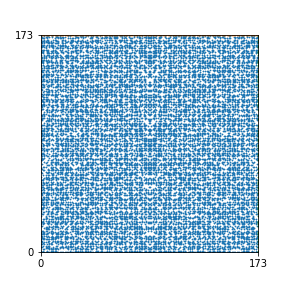
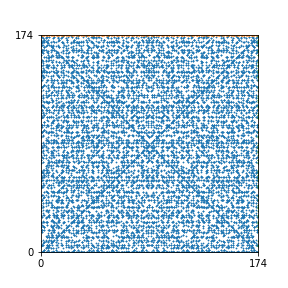
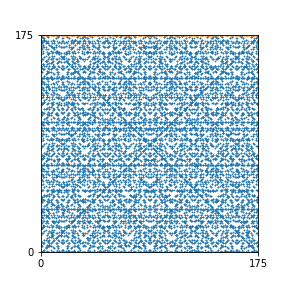
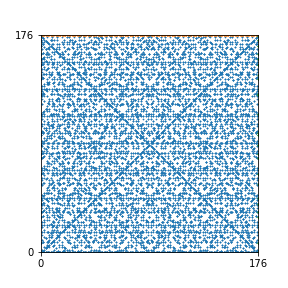
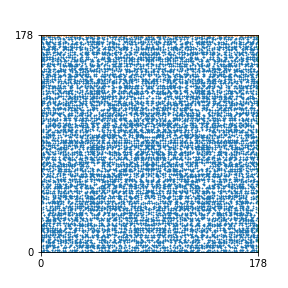
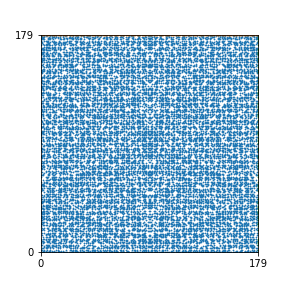
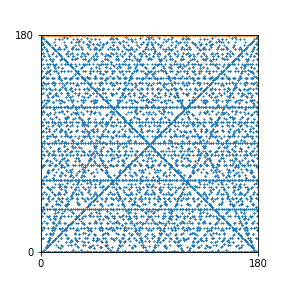
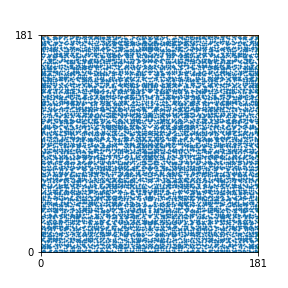
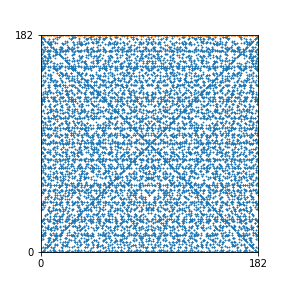
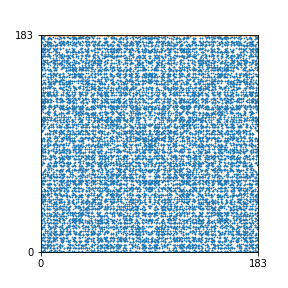
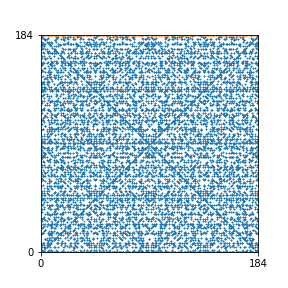
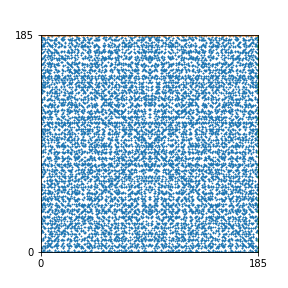
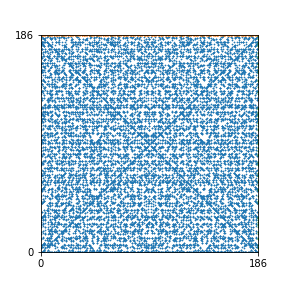
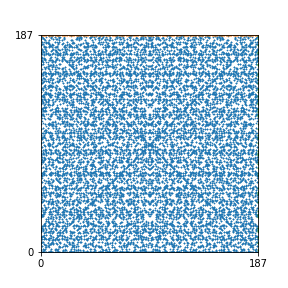
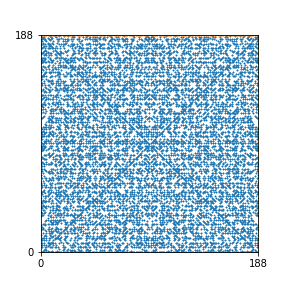
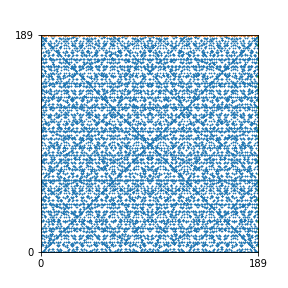
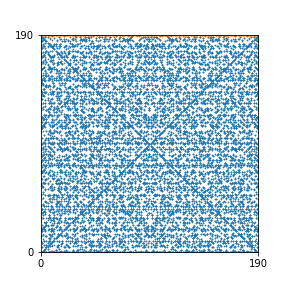
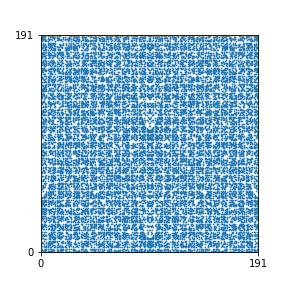
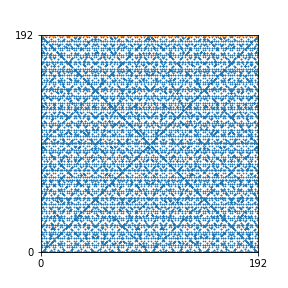
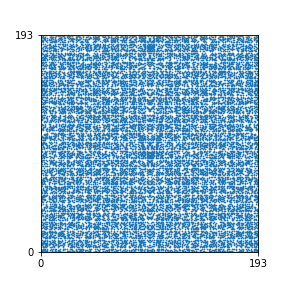
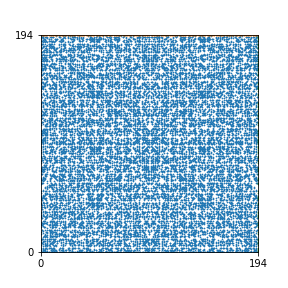
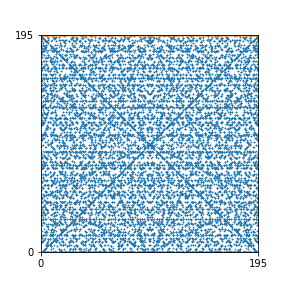
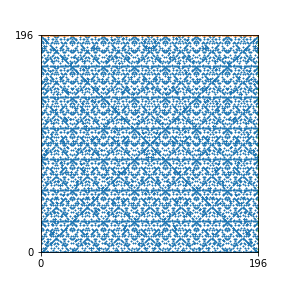
And here is the Python code. I run this inside a Jupyter notebook.

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from itertools import product

for n in range(2,200):
    N1=1   # number of times the pattern is repeated horizontally
    N2=1   # number of times the pattern is repeated vertically
    numberofdots = N1*N2*(n*n + n)/2       # estimate (!) of number of dots
    d = 1.1
    s0 = 10000.0/pow(numberofdots,d)       # area of each dot should decrease for larger number of dots
    l = list(range(n))                     # list of numbers modulo p

    b_list = [x_1+x_2  for x_1,x_2 in product(l,l)]        # b-coefficients of reducible polynomials
    c_list = [x_1*x_2  for x_1,x_2 in product(l,l)]        # c-coefficients of reducible polynomials

    # convert to numpy arrays
    b = np.asarray(b_list)
    c = np.asarray(c_list)

    # plot layout
    axes = plt.gca()
    axes.set_aspect('equal','box')
    axes.set_xlim([0,N1*n])
    axes.set_ylim([0,N2*n])
    plt.xticks([0,n])
    plt.yticks([0,n])

    # scatter plotting all dots, each with the correct size
    for i in range(N1+1):
        for j in range(N2+1):
            plt.scatter(n*i + b % n, n*j + c % n, s=s0)
            
    plt.show()

To estimate the number of dots in each “block” of the pattern, I use the formula \((n^2+n)/2\). This is the exact number of dots if \(n\) is a prime number, but an overestimate otherwise. As a result, the patterns for prime numbers are more “dense”.

The number of dots per block for the first few patterns are 3,6,8,15,18 and 28 (you can count them in the images above). So we search for “3,6,8,15,18,28” in The On-Line Encyclopedia of Integer Sequences (OEIS). The sequence that we need is Sequence A261928. We could use this to “repair” the estimate in the code, but I don’t think that would make the pictures more interesting.